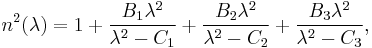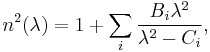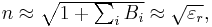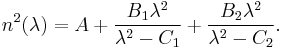Sellmeier equation

The Sellmeier equation is an empirical relationship between refractive index and wavelength for a particular transparent medium. The equation is used to determine the dispersion of light in the medium.

It was first proposed in 1871 by Wolfgang Sellmeier, and was a development of the work of Augustin Cauchy on Cauchy's equation for modelling dispersion.

Contents

The equation

The usual form of the equation for glasses is

n^2(\lambda) = 1 %2B \frac{B_1 \lambda^2 }{ \lambda^2 - C_1} %2B \frac{B_2 \lambda^2 }{ \lambda^2 - C_2} %2B \frac{B_3 \lambda^2 }{ \lambda^2 - C_3},

where n is the refractive index, λ is the wavelength, and B1,2,3 and C1,2,3 are experimentally determined Sellmeier coefficients.[1] These coefficients are usually quoted for λ in micrometres. Note that this λ is the vacuum wavelength; not that in the material itself, which is λ/n(λ). A different form of the equation is sometimes used for certain types of materials, e.g. crystals.

As an example, the coefficients for a common borosilicate crown glass known as BK7 are shown below:

Coefficient Value
B1 1.03961212
B2 0.231792344
B3 1.01046945
C1 6.00069867×10−3 μm2
C2 2.00179144×10−2 μm2
C3 1.03560653×102 μm2

The Sellmeier coefficients for many common optical glasses can be found in the Schott Glass catalogue, or in the Ohara catalogue.

For common optical glasses, the refractive index calculated with the three-term Sellmeier equation deviates from the actual refractive index by less than 5×10−6 over the wavelengths range of 365 nm to 2.3 µm,[1] which is of the order of the homogeneity of a glass sample.[2] Additional terms are sometimes added to make the calculation even more precise. In its most general form, the Sellmeier equation is given as

n^2(\lambda) = 1 %2B \sum_i \frac{B_i \lambda^2}{\lambda^2 - C_i},

with each term of the sum representing an absorption resonance of strength Bi at a wavelength √Ci. For example, the coefficients for BK7 above correspond to two absorption resonances in the ultraviolet, and one in the mid-infrared region. Close to each absorption peak, the equation gives non-physical values of 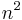n^2=±∞, and in these wavelength regions a more precise model of dispersion such as Helmholtz's must be used.

If all terms are specified for a material, at long wavelengths far from the absorption peaks the value of n tends to

\begin{matrix} n \approx \sqrt{1 %2B \sum_i B_i } \approx \sqrt{\varepsilon_r} \end{matrix},

where εr is the relative dielectric constant of the medium.

The Sellmeier equation can also be given in another form:

n^2(\lambda) = A %2B \frac{B_1 \lambda^2}{\lambda^2 - C_1} %2B \frac{ B_2 \lambda^2}{\lambda^2 - C_2}.

Here the coefficient A is an approximation of the short-wavelength (e.g., ultraviolet) absorption contributions to the refractive index at longer wavelengths. Other variants of the Sellmeier equation exist that can account for a material's refractive index change due to temperature, pressure, and other parameters.

Coefficients

Table of coefficients of Sellmeier equation[3]
Material B1 B2 B3 C1 C2 C3
borosilicate crown glass
(known as BK7)		 1.03961212 0.231792344 1.01046945 6.00069867×10−3µm2 2.00179144×10−2µm2 1.03560653×102µm2
sapphire
(for ordinary wave)		 1.43134930 0.65054713 5.3414021 5.2799261×10−3µm2 1.42382647×10−2µm2 3.25017834×102µm2
sapphire
(for extraordinary wave)		 1.5039759 0.55069141 6.5927379 5.48041129×10−3µm2 1.47994281×10−2µm2 4.0289514×102µm2
fused silica 0.696166300 0.407942600 0.897479400 4.67914826×10−3µm2 1.35120631×10−2µm2 97.9340025 µm2

See also

References

  1. ^ Refractive index and dispersion. Schott technical information document TIE-29 (2007).

External links